Verlet Physics Engine
Petite mise en bouche
 |
 |
|---|
Table des matières
- Intégration d’Euler
- Intégration de Verlet
- Implémentation
- Résultats finaux
- Outils utilisés
- Références
Intégration d’Euler
La majorité des moteurs de jeux qui offrent de l’interaction physique font appel à l’intégration d’Euler qui est une méthode numérique de résolution d’équations différentielles du premier ordre.
L’implémentation rudimentaire consiste à, pour chaque objet, attribuer une position, vitesse et accélération, et à chaque itération de la simulation, ajouter la vitesse à la position et l’accélération à la vitesse.
update():
position += velocity * dt
velocity += acceleration * dt
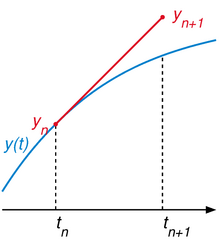
Cette méthode est relativement simple à implémenter et offre de bonne performances, cependant celle-ci a tendance à être instable. La cause étant qu’avec la simulation numérique, il est impossible d’avoir de la simulation continue, nous sommes donc contraint de faire avancer la simulation d’un pas de temps donné dt (dans le cas d’une simulation à 60Hz, 1/60 ms, soit 0.017ms), ce qui introduit de l’imprécision dans les calculs de trajectoire.
Voici une comparaison des deux méthodes :

C’est pourquoi nous allons explorer l’implémentation d’un moteur physique faisant appel à l’intégration de Verlet.
Intégration de Verlet
L’intégration de Verlet consiste à déduire la nouvelle position à partir de la position actuelle et de la position précédente (donc la vélocité indirectement).
update()
new_pos = 2*pos - old_pos + acceleration * dt²
old_pos = pos
La vélocité n’étant pas stockée en dur, le système est de facto plus stable.
Pour rendre les choses moins glissantes, il suffit d’ajouter un facteur de friction lors de la mise à jour de la position.
Implémentation
Système de particule
Les moteurs de simulation physique utilisent un système de particules.
L’utilisation de la méthode de Verlet rend cette implémentation relativement simple.
Voici un premier rendu avec le traçage d’une unique particule auquel on a appliqué de la gravité et une “vélocité” initiale. À noter que pour empêcher la particule de sortir de la zone, une simple contrainte [min, max] sur ses coordonnées suffit.
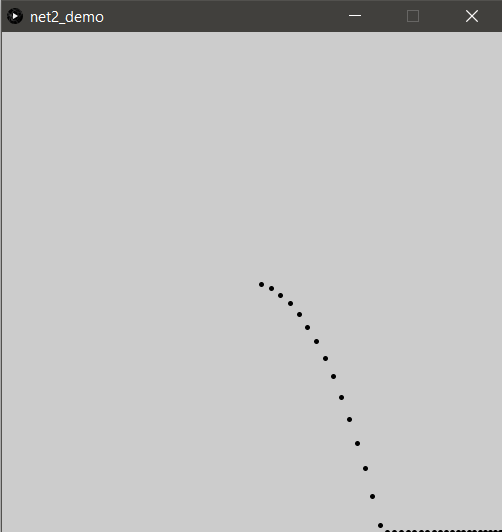
Là où les choses deviennent intéressante, c’est lors de l’ajout de contraintes entre les particules.
Contrainte bâton
La contrainte la plus basique est la “stick constraint” ou contrainte bâton. Elle va nous permettre de construire tout type de formes géométriques.
Celle-ci consiste à enforcer la conservation d’une distance initiale entre deux particules.
Pour satisfaire cette contrainte, il suffit alors d’ajouter le décalage nécessaire afin de rapprocher ou d’éloigner les deux particules.
delta = p2 - p1
delta_length = sqrt(dot(delta, delta))
ratio = (delta_length - init_length) / init_length
p1 -= delta * ratio / 2
p2 += delta * ratio / 2
Voici un rendu d’une simple contrainte entre deux particules : un joli bâton !
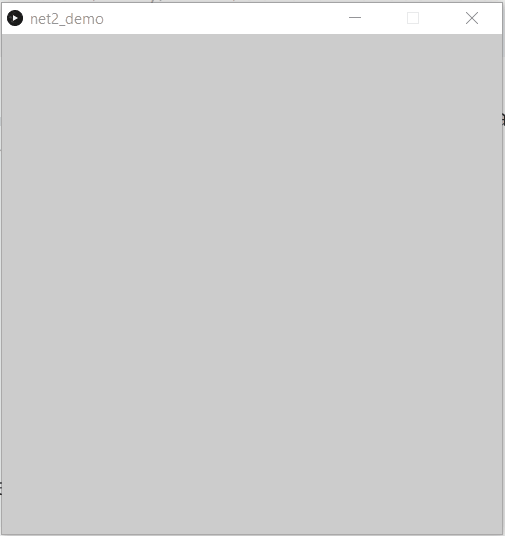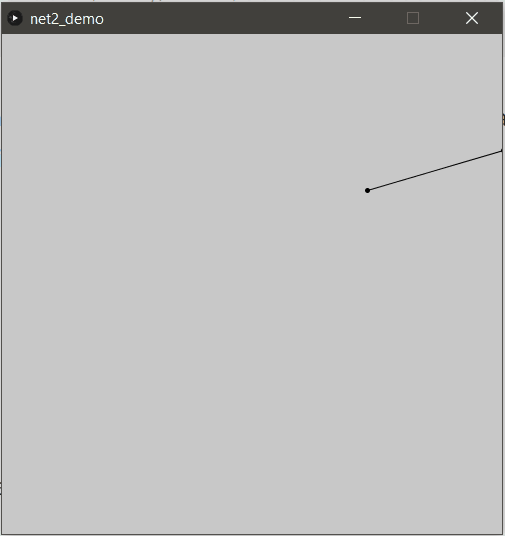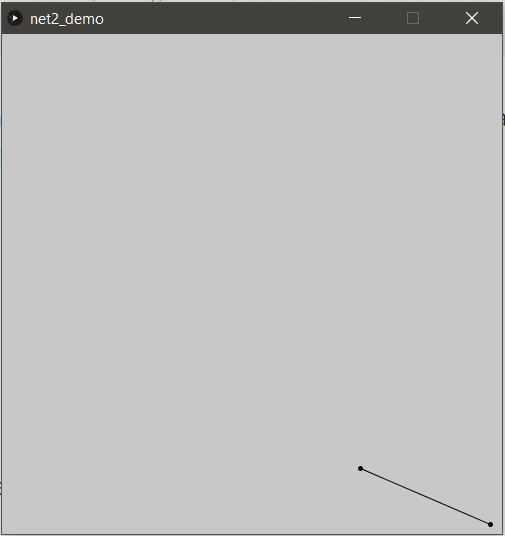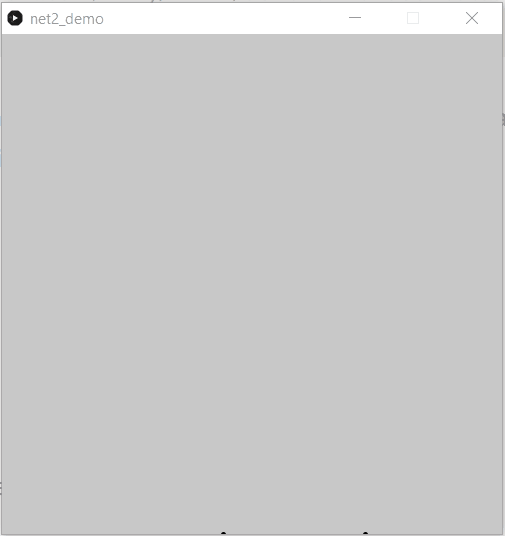
L’avantage de cette approche que l’on constate immédiatement est qu’aucun traitement particulier n’est nécessaire pour la rotation !
En mettant bout à bout plusieurs de ces contraintes : une chaîne !
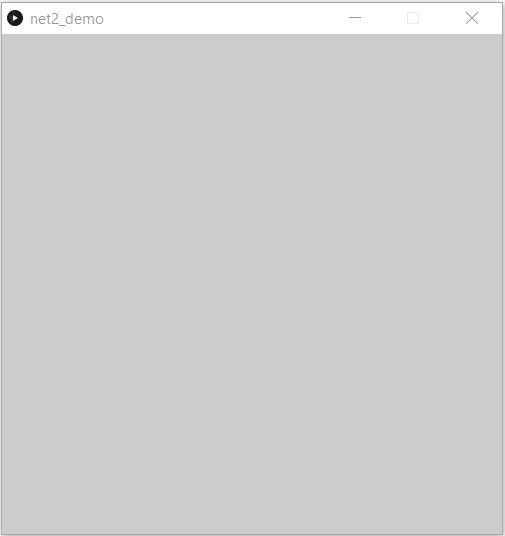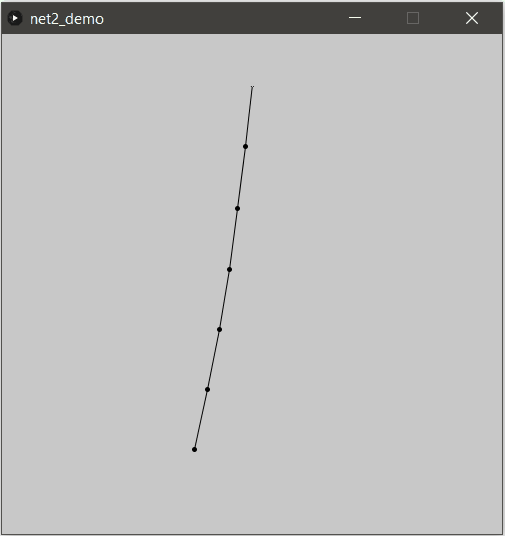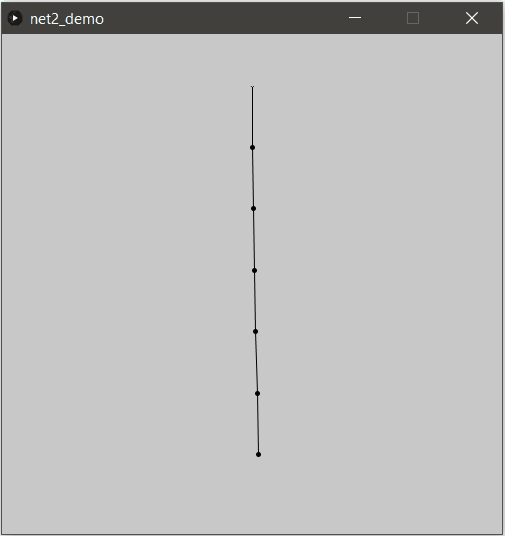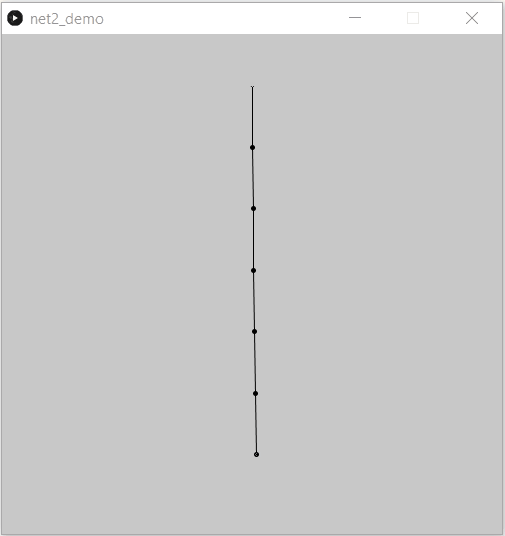
Modèle du solide indéformable (Rigid body)
Comme dit précédemment, avec ce type de contrainte, nous sommes en mesure de créer des formes géométriques.
Pour ce faire, il est préférable de regrouper les différents points et contraintes qui constituent la pièce au sein d’un même objet, plus communément appelé “rigid body”.
Ce regroupement permettra de manipuler les pièces individuellement, ce qui va s’avérer pratique comme nous allons bientôt le voir.
Cependant ici quelque chose ne va pas. La pièce ne semble pas rigide !
Le soucis est que les contraintes ne sont pas résolues assez rapidement, ce qui donne cette impression de “mou”. Pour contrer ce problème, il suffit alors de résoudre les contraintes plusieurs fois par itération. Cela a évidemment un coût, mais en général un petit nombre d’itérations suffit amplement.
update()
updateParticles()
for 1 to 3
resolveConstraints()
Voici le même triangle, avec 3 itérations pour la résolution de contraintes :
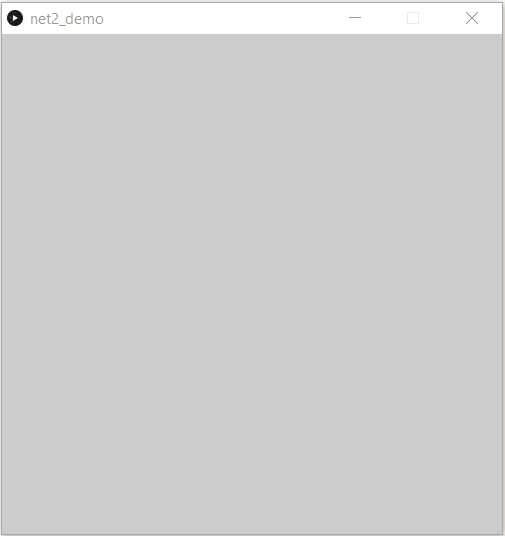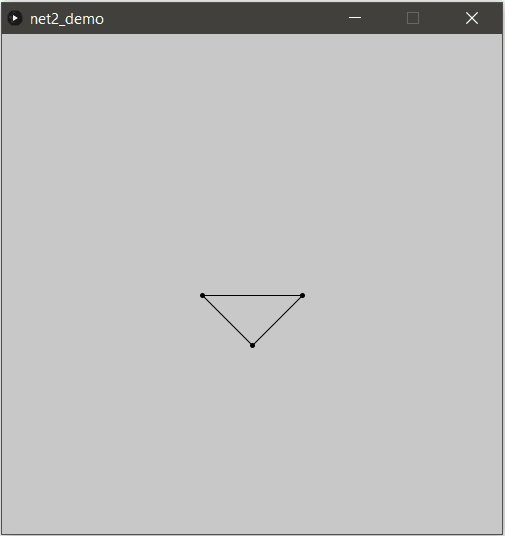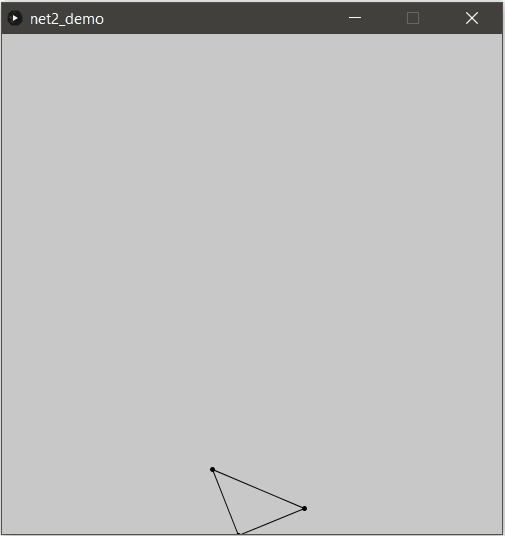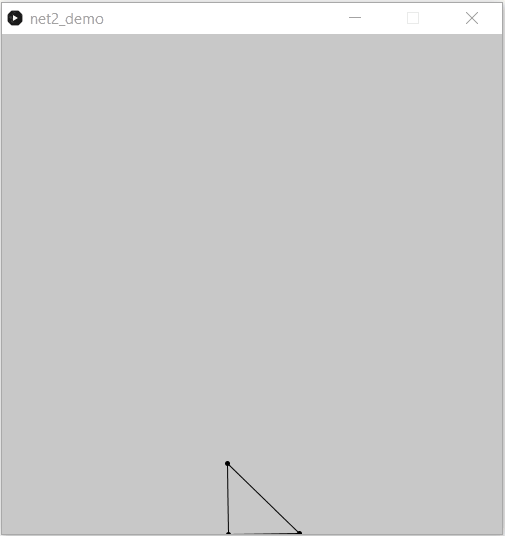
Essayons maintenant avec plus de points, trivial non ?
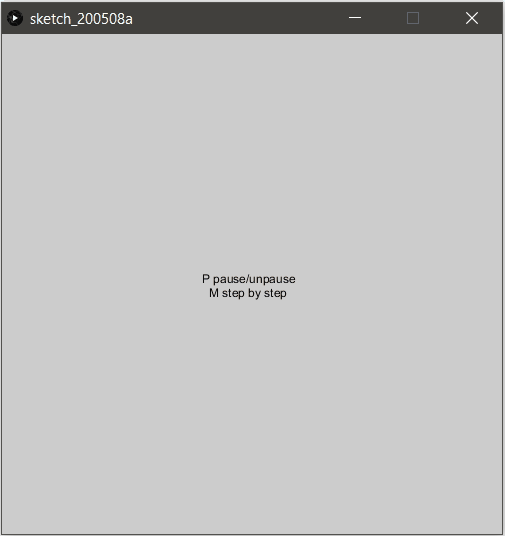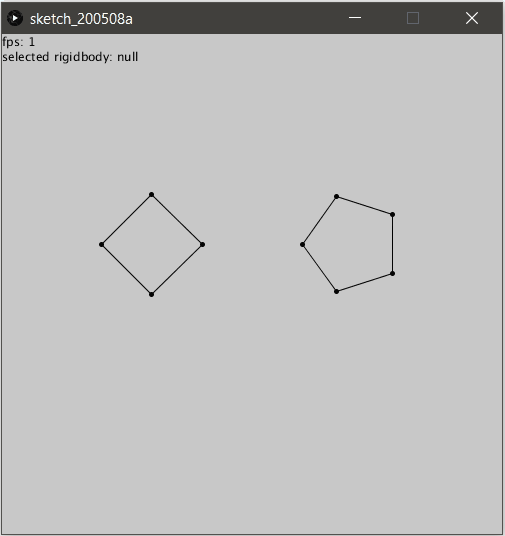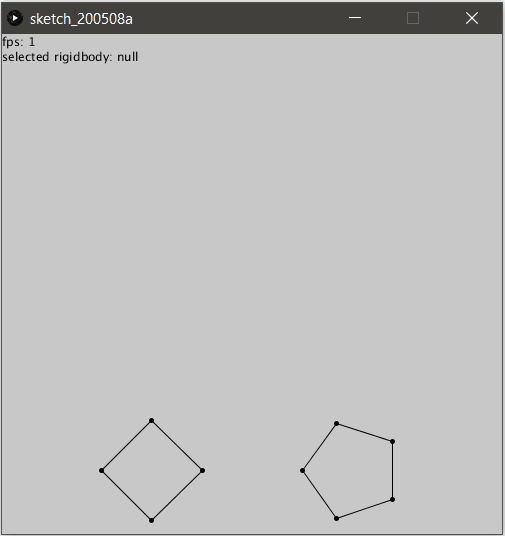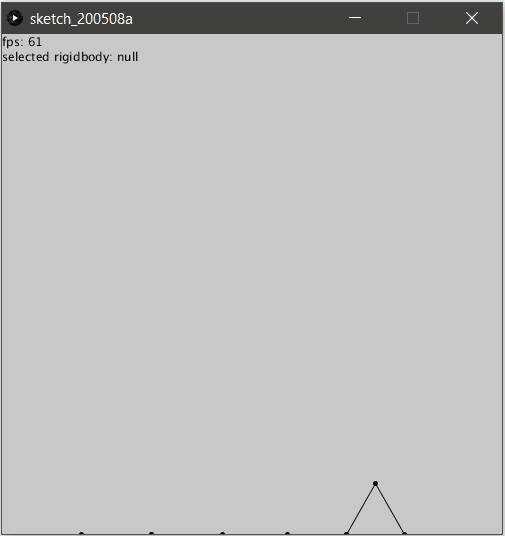

Peut être pas si simple…
En réalité, il suffit d’ajouter des “supports” qui ne sont rien d’autres que des contraintes bâtons placées stratégiquement au sein de l’objet !
Les voici affichées en couleur pour mieux comprendre :
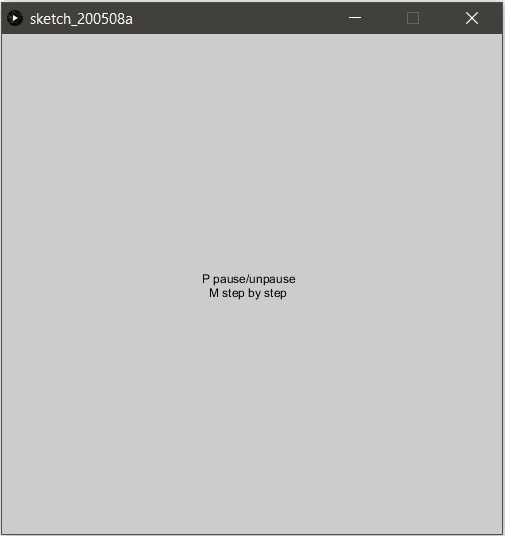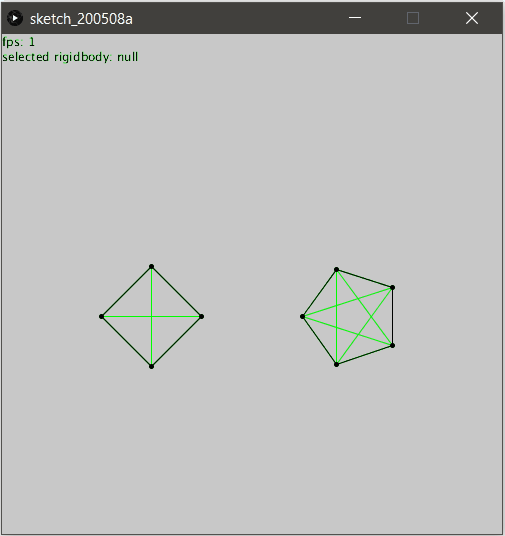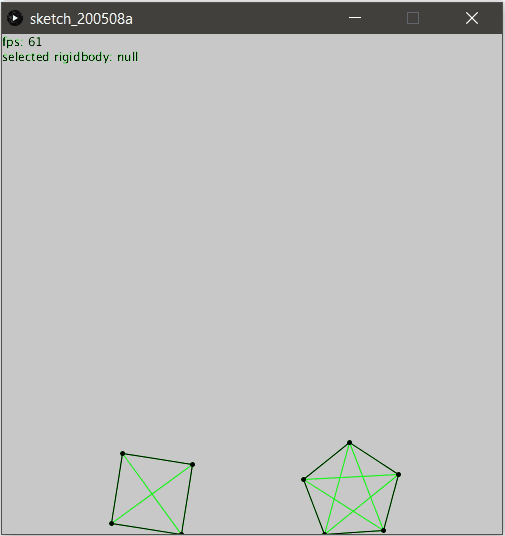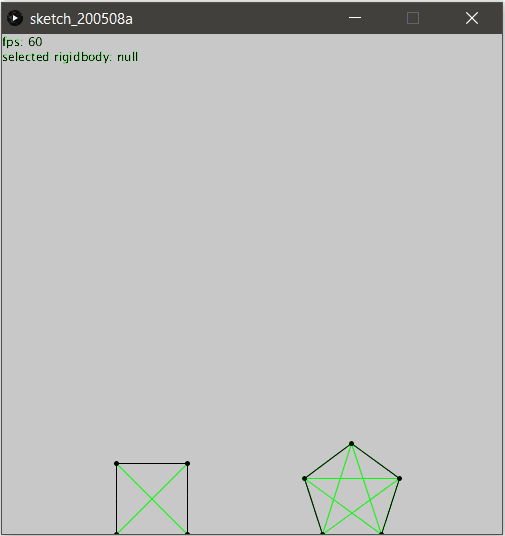
Pour obtenir l’illusion parfaite, il suffit alors de ne pas les afficher :
(nous pouvons ignorer les particules aussi au passage)
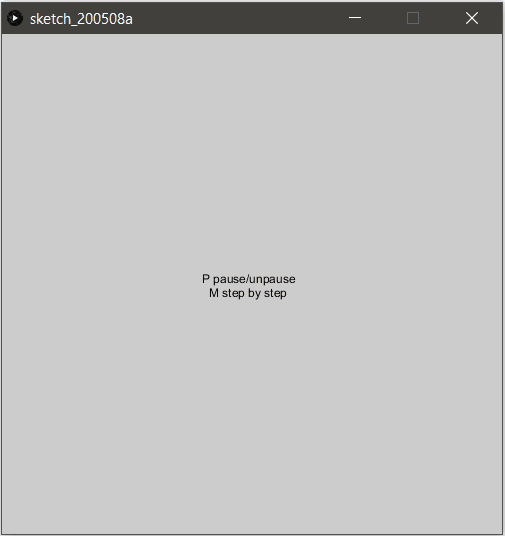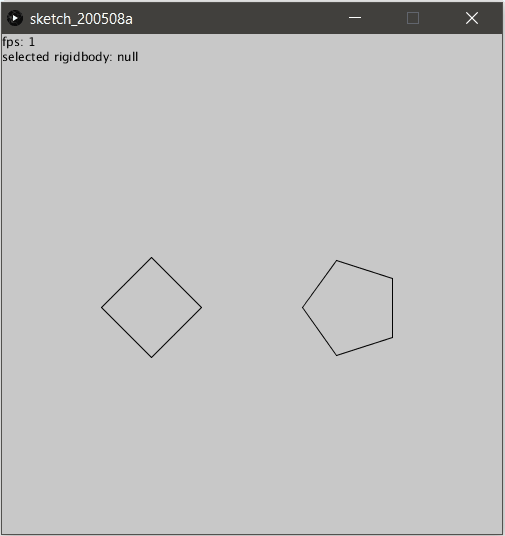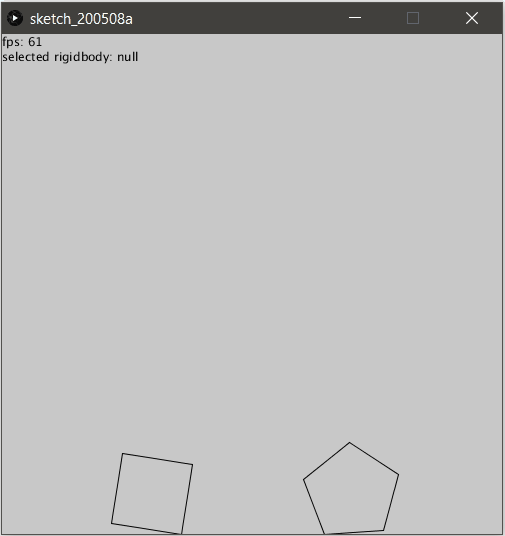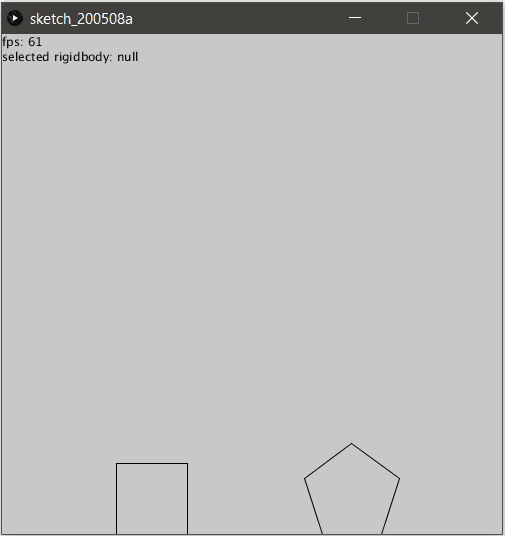
Collision
Hum Houston, il y a un petit problème là je crois…
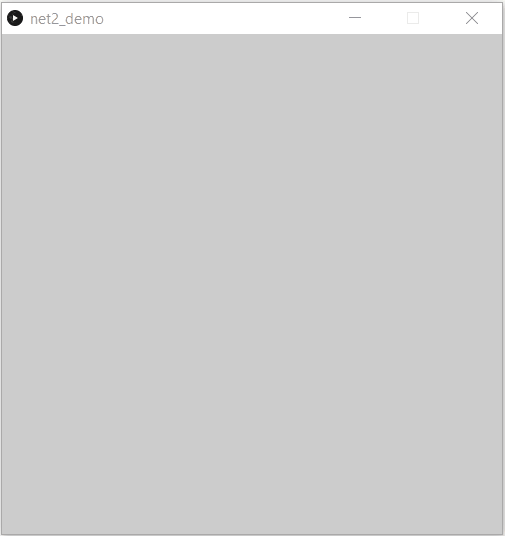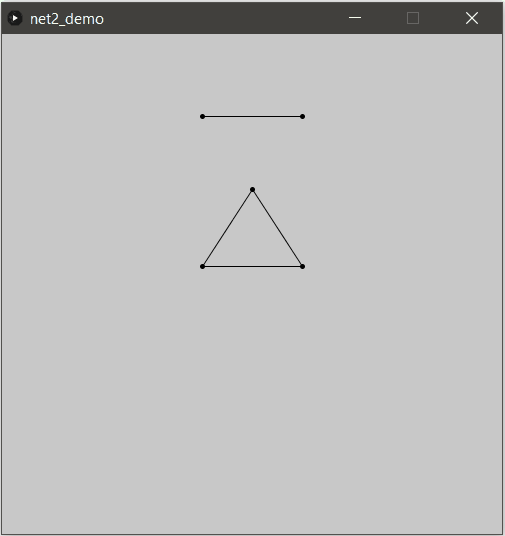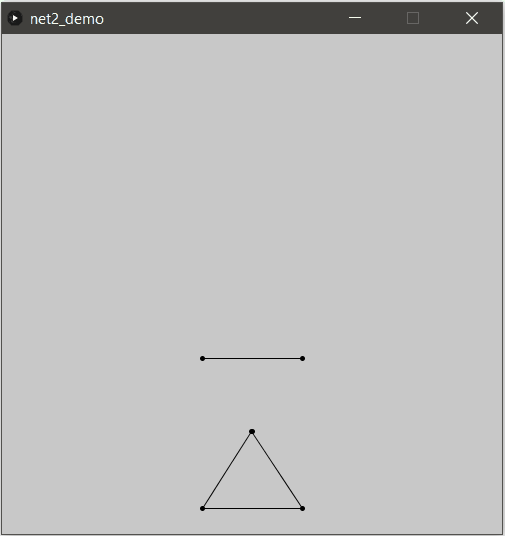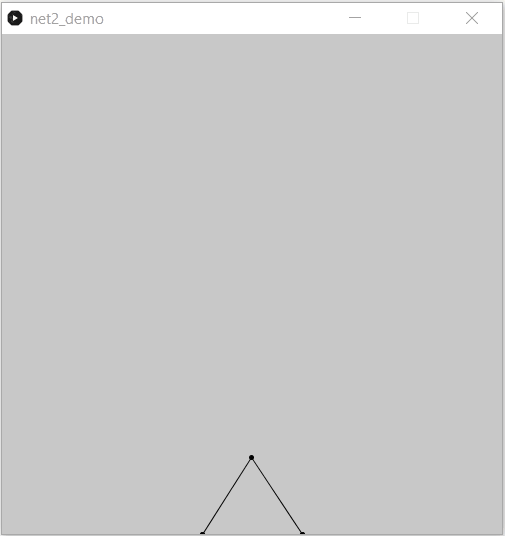
Cette méthode n’est pas non plus magique, il faut gérer la collision entre pièces !
Le papier originel explique vaguement comment résoudre les collision, mais je n’ai pas été en mesure de l’implémenter.
Je me suis donc rabattu sur une méthode alternative qui semble fonctionner correctement, cependant celle-ci ne gère pas les formes convexes.
La première étape pour la résolution de collision consiste d’abord à détecter ainsi que d’extraire des information de la collision.
Détection de collision (Méthode des diagonales)
Il existe une multitude des méthodes de détection de collision 2D (AABB, SAT, etc.), cependant celles ci agissent sur une pièce dans son ensemble, ce qui ne se prête pas bien à notre implémentation faisant appel à un système de particules.
C’est pourquoi j’ai déniché une méthode tierce, celle-ci ne semble pas avoir de nom concret, mais elle fait appel aux diagonales des pièces, j’y ferai donc référence sous le nom de “méthode des diagonales” désormais.
Cette méthode permet d’étudier la collision entre la diagonale d’une pièce et l’arrête d’une autre pièce.
p1: centre de la pièce n°1
p2: particule de la pièce n°1
q1 et q2: particules formant le segment de la pièce n°2
Voici des schémas pour mieux comprendre :
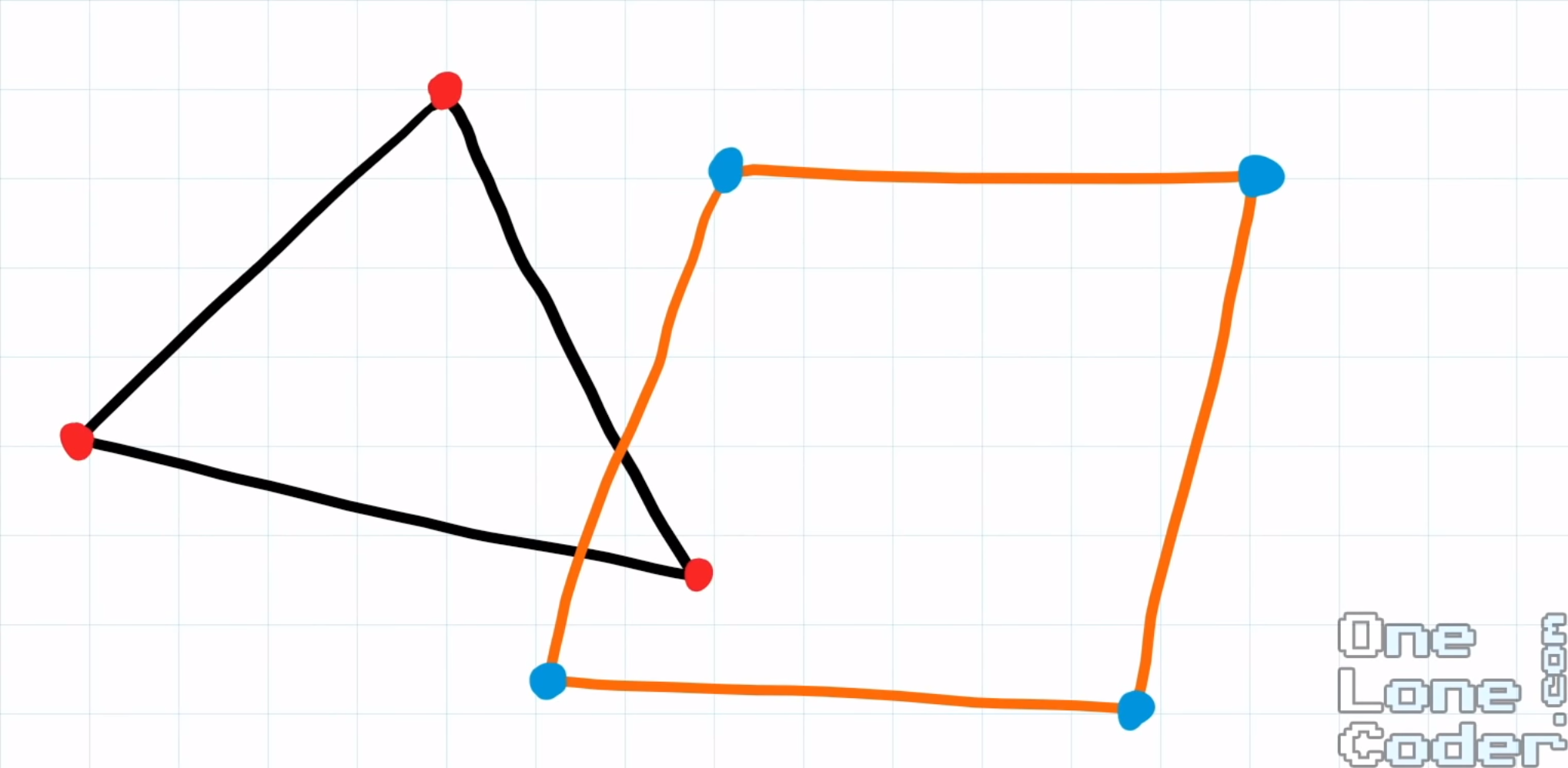 situation initiale situation initiale |
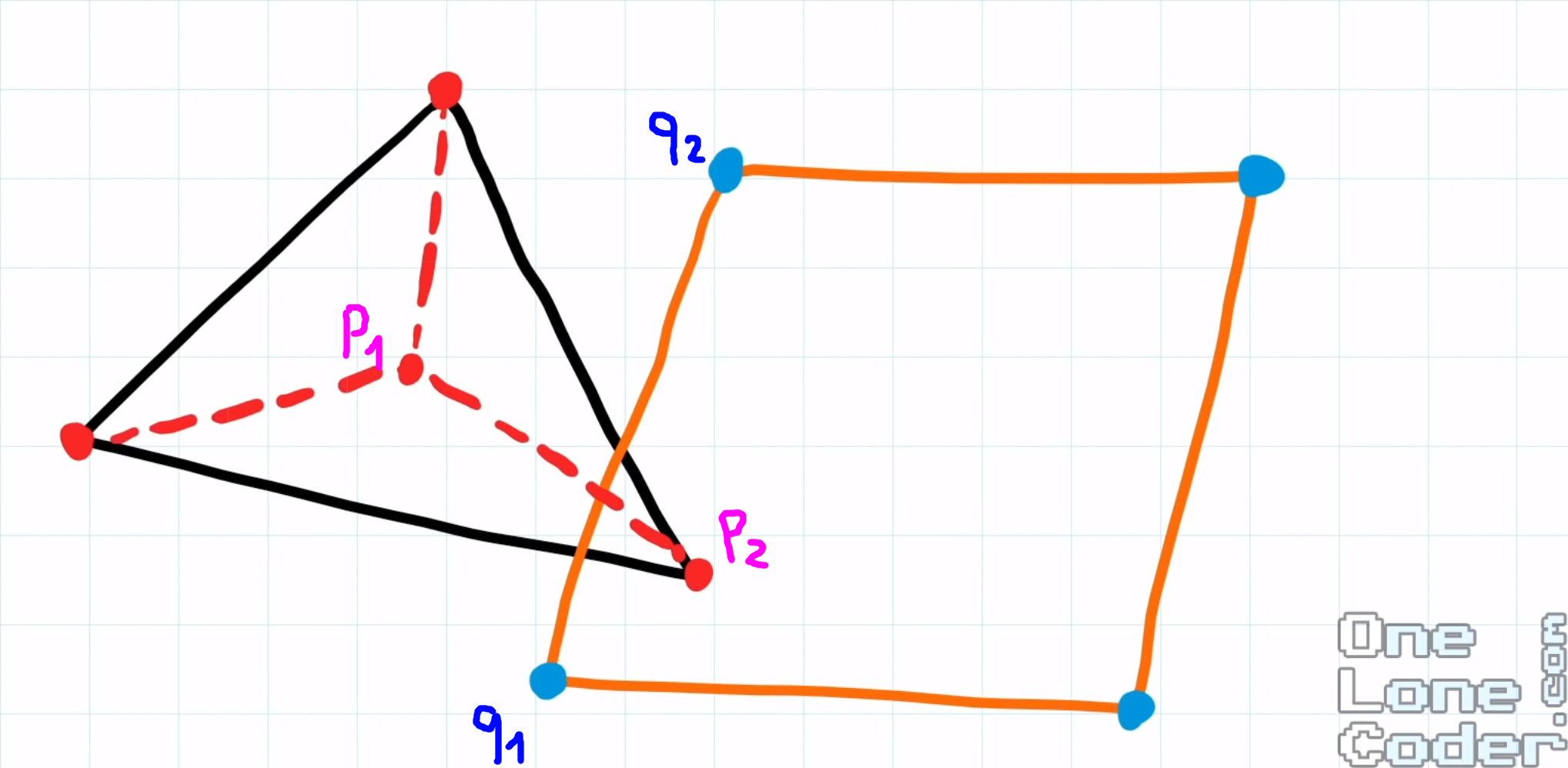 en rouge les diagonales de la pièce n°1 en rouge les diagonales de la pièce n°1 |
|---|
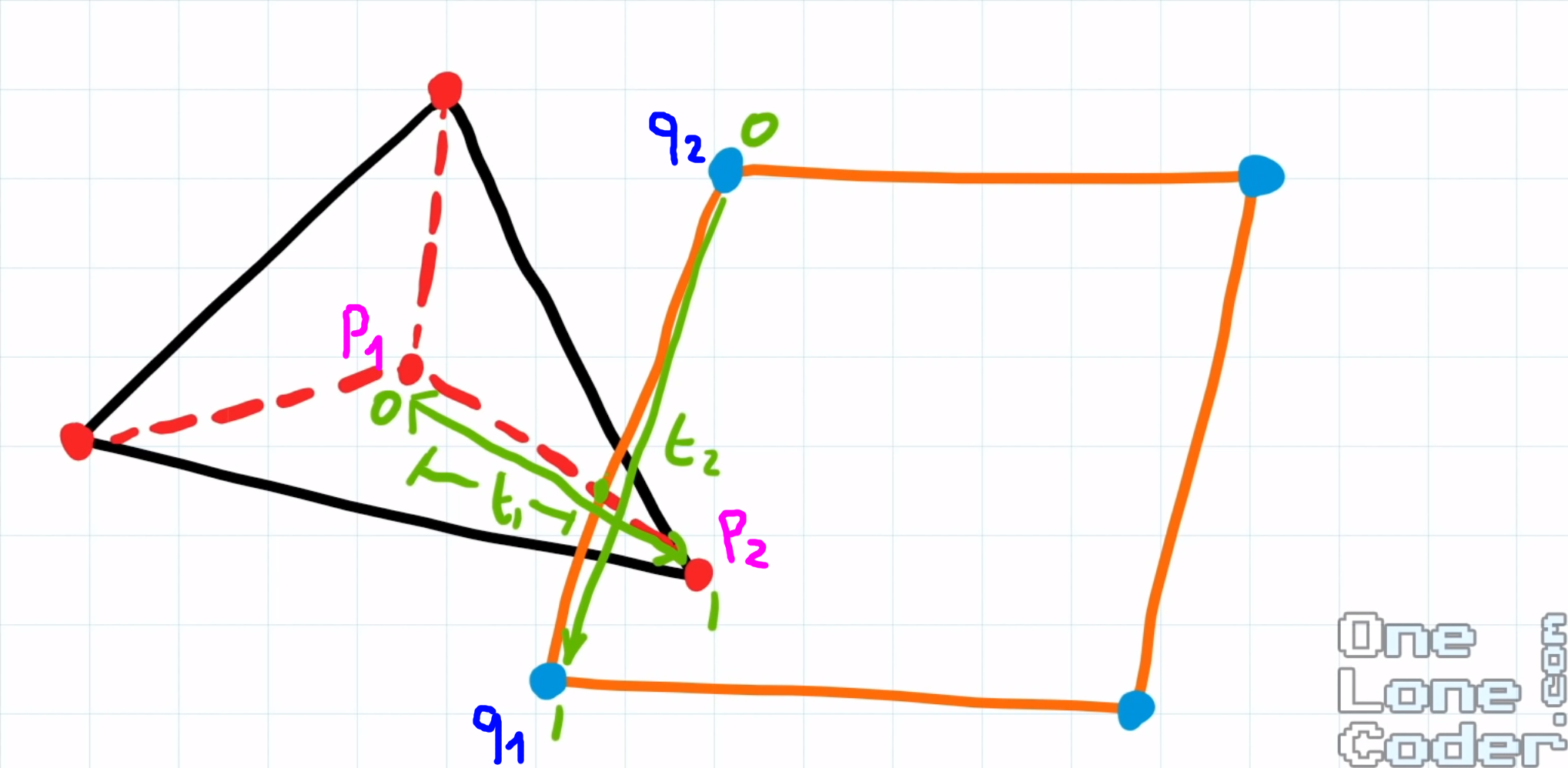 intersection (en vert) d’une des diagonales de la pièce n°1 avec une des arrêtes de la pièce n°2 intersection (en vert) d’une des diagonales de la pièce n°1 avec une des arrêtes de la pièce n°2 |
|---|
Le troisième schéma montre l’utilisation d’un algorithme de détection de collision entre deux segments, que voici :
// Given a segment (p1, p2) and another segement (q1, q2)
// Returns whether they collide or not
do_line_intersect()
h = (q2.x - q1.x) * (p1.y - p2.y) - (p1.x - p2.x) * (q2.y - q1.y)
t1 = ((q1.y - q2.y) * (p1.x - q1.x) + (q2.x - q1.x) * (p1.y - q1.y)) / h
t2 = ((p1.y - p2.y) * (p1.x - q1.x) + (p2.x - p1.x) * (p1.y - q1.y)) / h
return (t1 >= 0.0f && t1 < 1.0f && t2 >= 0.0f && t2 < 1.0f):
Une fois les informations de la collision obtenues, il ne reste plus qu’à la résoudre !
Résolution de collision
À l’aide des facteurs t1 et t2 obtenus lors de la détection de collision, nous sommes en mesure de résoudre la collision en agissant sur les 3 particules en formant ces deux segments.
Le facteur t1 représente représente la position du point d’intersection le long de la diagonale de la pièce n°1. Celui-ci nous donne la profondeur de la collision (1 - t1).
Le facteur t2 représente représente la position du point d’intersection le long de l’arrête de la pièce n°2. Celui-ci va nous permettre de répartir les déplacements à appliquer aux particules de manière à avoir un résultat cohérent.
normal = (-(q1.y - q2.y), q1.x - q2.x)
penetration_ratio = 1 - t1
peneration = normal * penetration_ratio
p2 += peneration * 0.5
q1 -= peneration * 0.5 * (1 - t2)
q2 -= peneration * 0.5 * t2
Et après plusieurs heures à se taper la tête contre un mur : TADA !

Résultats finaux
Après l’ajout d’un simple système d’interaction avec les objets, les choses deviennent d’autant plus amusantes.


Les possibilités sont infinies. D’autres types de contraintes existent. Je vous recommande fortement d’essayer par vous même si cela vous a plu !
Outils utilisés
J’ai utilisé Processing pour ce projet. C’est un logiciel ainsi qu’un langage (basé sur Java) qui rend la création de contenu graphique extrêmement simple, ce fut donc un choix parfait pour ce petit projet !
Références
Verlet integration
https://en.wikipedia.org/wiki/Verlet_integration
A Simple Time-Corrected Verlet Integration Method
http://archive.gamedev.net/archive/reference/articles/article2200.html
Advanced Character Physics
https://www.cs.cmu.edu/afs/cs/academic/class/15462-s13/www/lec_slides/Jakobsen.pdf
Convex Polygon Collisions
https://www.youtube.com/watch?v=7Ik2vowGcU0
